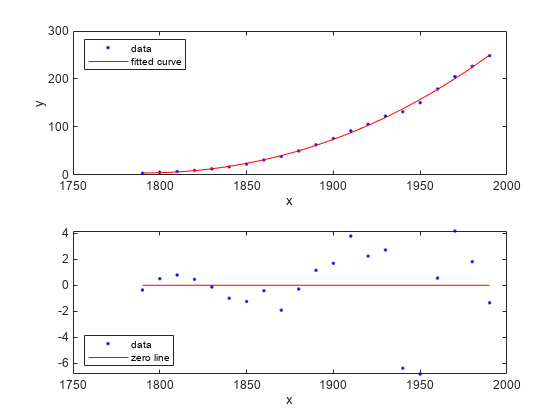
이전 문장을 읽고 있지 않은 경우는 예전의 글에서 먼저 읽어 보길 권합니다.우선 켈리 공식 AtoZ시리즈를 시작하기 전에… 그렇긴 신용 자산에 얼마나 투자할지를 배분한다는 것을 비유해서 봅시다.복수의 자산 군은 경마에 참여하는 말입니다.그리고 자산 배분을 한다는 것은 결국 마권을 얼마나 사느냐를 결정짓는 행위와 같습니다.다양한 자산 군의 가격이 좋아지고, 많이 호전될수록 우승한다면?그 해당 자산에 대해서 마권을 배분하는 것을 가장 효율적으로 실시한다면?우승할 확률과 배당이 높은 쪽에 집중하고 주었다( 믿는 만큼 행사)방식이 케리 공식대로 배분하겠지요.균등 배분=마권을 자산 군마다 같은 비율로 마권을 사다.최소 분산=표준 편차와 기대 수익률을 예상하고 최대한 배당금 대비 흔들리지 않도록 예상되는 비중에서 마권을 사다.위험 균형=특정 자산이 갖는 위험 비중을 계산하고, 이를 고려하고 위험 비율을 동일한 비율로 마권을 사다.켈리 공식(기하 평균)=위험은 전부 무시하고 가장 잘하려고 자산에 대부분의 마권을 사다.그래서 켈리 공식대로 자산을 최적화하면 결국 최고 자산 군에 상당수 집중시키는 결과가 나오게 됩니다.그것을 최적화하면 위험을 아랑곳하지 않고 가장 잘 팔리는 자산 군에만 집중시키는 결과가 나오게 되고, 적당한 최적화하는 방법이 필요합니다.최적화하는 방법에는 여러가지 방법이 있지만
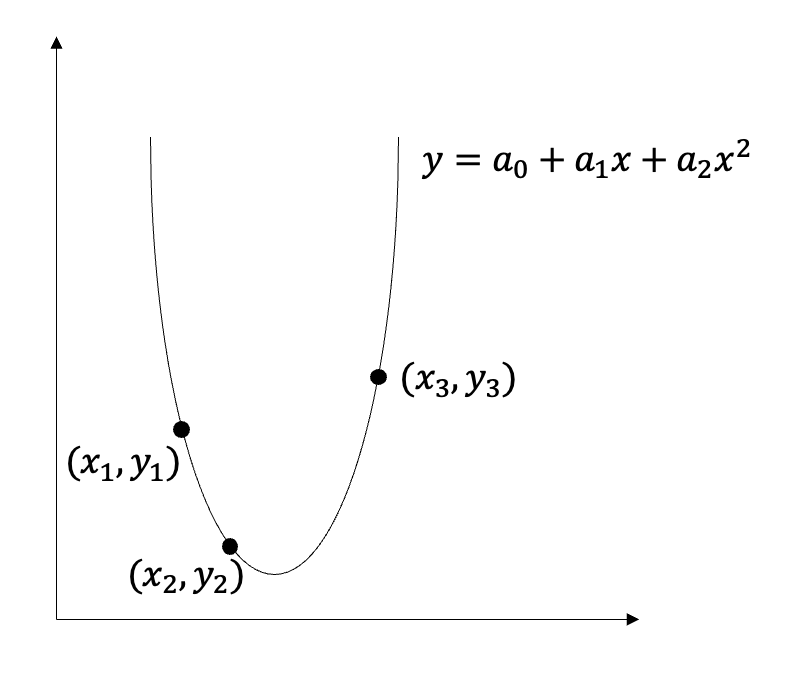
유전 알고리즘으로 최적화한다면? 적당히 근사치로 빠르게 가구 수를 적당히 하면서 관찰하는 것이 가능하지만

각 전략 or 자산군 수익률 이산 분포 행렬이 있다면?

유전 알고리즘을 활용했기 때문에 매번 전략을 투자하는 비율과 그 성과를 선택할 수 있습니다.(할 때마다 다름)

curve fitting은 아니지만 변화성=동일 가중>kelly(극단이 아니라 적당한 최적화)>single best성과=single best>kelly(극단이 아니라 적당한 최적화)>동일 가중인 것으로 확인할 수 있습니다.그네의 영상처럼 많은 최적화하면 결국 가장 잘 팔리는 자산인 오렌지 색 라인에 가까운 1개 자산 군에 비중을 많이 올린 최적화 되고 그렇다고 그냥 한 곳에 집중하려고 분산 효과를 누리지 못하므로 적당하게 최적화되는 것이 중요하죠.그리고 이것도 어차피 In-sample속에서 다시 최적화한 것이어서 향후 Out of sample에서 수익 곡선이 비슷하게 흘러가지 않으면 전혀 의미가 없어요.최적화하는 원리에 대해서 더 자세히 말해서 본다고?행렬(표)가 있다고 먼저 가정하고 보겠습니다.R11=첫날 전략 1에 대한 손익 명세[ex)그날 손익이 5%라면 0.05-10%라면-0.1]R12=2일째에 전략 1에 대한 손익 명세···Rnm개의 요소가 있습니다.전략 or자산 군은 n개, 자금 투입당의 거래 손익 내역 m개가 있다고 가정합니다.그렇게 되자 전략에 대한 X행렬을

이렇게 생각하실 수도 있고, 반대로 전략n종에 대한 자금거래일당 손익내역을 Y행렬로 생각하실 수도 있습니다..
또 자금 투입 비율 f1~fn(마권 배분 비율)에 대한 행렬 F도 생각해 보겠습니다.
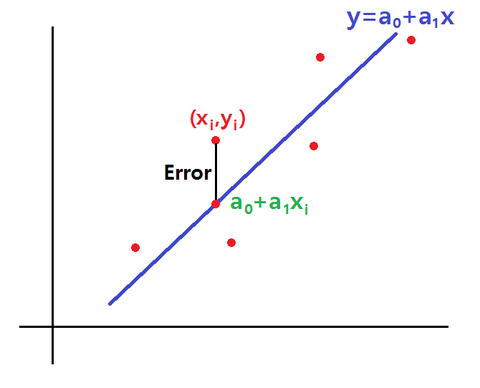
최적화된 f의 비율을 찾으려면 log(1+Y·F[transpose])에서 f1에서 fn까지 배분 비율을 변경시키고 투입하면서 log(1+Y·F[transpose])이 가장 비싼 값이 나오는 것이 케리 공식적으로 최적화하는 법입니다.(위 그래프는 그 방법을 유전자 알고리즘에서 최적화한 것)f1, f2,…, fn의 자산 군(or전략)배분 비율을 각각 0.01~1까지 1%의 비율로 변경하면서 나올 경우의 수는 100^(n-1) 하므로 자산 수가 많으면 많을수록 경우의 수는 한층 늘어납니다.그런데 최적화를 하고 보면 자산 군이 많은 것이 중요한 것도 아니고 너무 적은 비중을 올려도 문제로 많이 올렸다고 해서 특별히 곡선 최적화(curve fitting)이라고 해서….공부를 그만둔 영역입니다.다만 자산 군 자체의 기본 투자 비율을 알고 싶다면 단일 자산 군 배분이 연속 분포에 있을 때(m-r)/(s)2)근사치 계산만으로도 충분하다고 생각합니다.
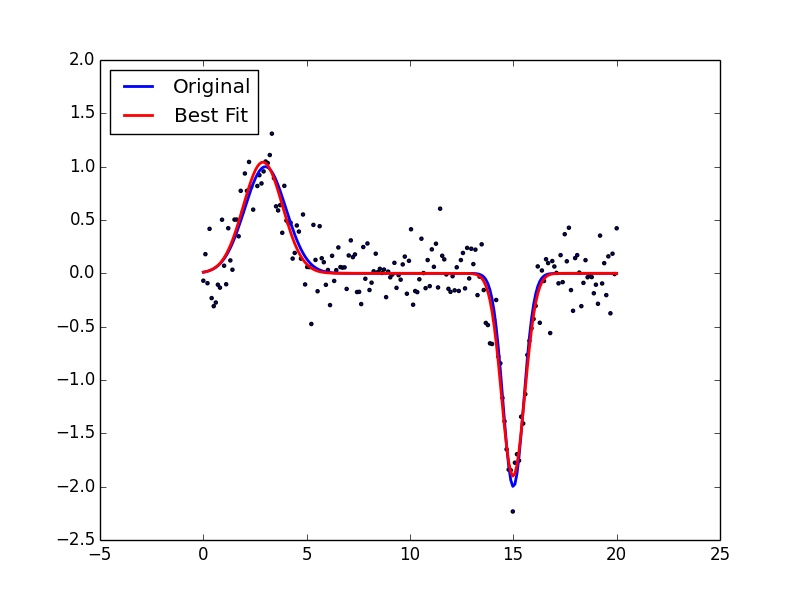
[켈리 공식 AtoZ]2.2연속 분포의 때의 켈리 공식.-에드워드 O.소후의 논문의 핵심을 보면 해당 글은 연재되고 있어 이전의 글을 읽고 있지 않은 경우는, 이전 글부터 읽어 보길 권합니다.우선 켈리 공식 AtoZ시리즈를 시작하기 전에… 그렇긴개인적으로 지금까지 이산 분포의 때의 공식 유도 과정을 정말 쉽게 설명했다고 생각합니다.그러나 연속 분포의 때의 켈리 공식 유도 과정을 좀 더 쉽게 설명하려면 좀 더 생각이 필요하다고 생각하니, 번외 편에서 다루기로 합니다.연속 분포의 경우는 어느 정도의 비율로 투자해야 할지에 대한 내용은 켈리 공식보다는 케리 기준(kelly criterion)이라고 명명하는 것이 더 분명합니다.증명과… 그렇긴 gambari90.com

오늘 설명은 아래 링크된 문장인 단일 자산인 이산 분포도를 관련된 공식을 어떤 자산군(or 전략)에 어떤 비율로 배분할 것인가에 대해 넓힌 확장판이라고 생각하시면 됩니다.

[켈리 공식 AtoZ]1-6.4가지 경우를 고려한 켈리 공식 해당 글은 연재되고 있어 이전의 글을 읽고 있지 않은 분은 이전 글부터 읽어 보길 권합니다.우선 켈리 공식 AtoZ시리즈를 시작하기 전에… 그렇긴켈리 공식을 본격적으로 쓰고 보겠습니다.이런 상황이 있다고 4가지 경우로 나누어 보겠습니다”(4일 주식 시장을 관찰한 결과 위아래 가격의 가정을 제외)A.20%의 확률로 베팅 금액 2배 분을 받는다.B.30%의 확률로 베팅 금액만 받는다.C.40%의 확률로 베팅 금액의 절반 분량을 잃는다.D.10%의 확률로 돈 전액을 잃는다.이런 게임이 있다고 가정하고 보겠습니다… 그렇긴 gambari90.com

이로써 켈리 공식을 언제 사용할 필요가 있습니까?전제 조건 켈리 공식 사용하고 본다켈리 공식 이산 분포일 때 사용하고 본다켈리 공식 연속 분포의 때에 사용하고 본다켈리 공식 이산 분포의 때에 다중 자산(or전략)때 쓰고 보기 전 켈리 공식에 관한 기본적인 설명은 모두 한 것 같아요.나중에 기회가 있으면 Proebsting’s paradox나 생각하고 볼 문제에 대해서도 언급하고 봅시다.차기작[켈리 공식 AtoZ]번외 편.워런, 버핏이 2번도 주주 총회에서 언급한 논문?(1)